Portafolio Santiago Zapata IU Pascual Bravo

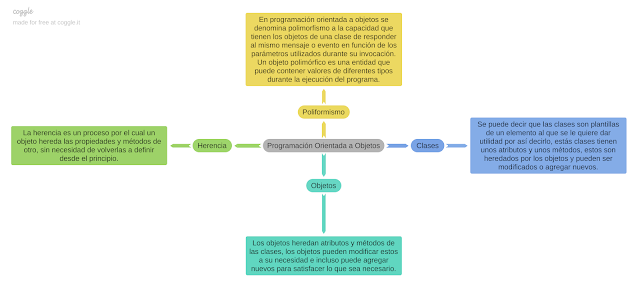
 Paradigma de la Programación Orientada a Objetos La programación orientada a objetos es una manera de programar diferente a los habitual, en esta se programa teniendo en cuenta de todo lo que se hace es enfocado o pensando en que se esta programando un objeto con características, atributos, métodos, etc. Cuando se aplica la programación orientada a objetos o POO, por sus iniciales, se debe de tener en cuenta que estos objetos hacen parte de una entidad mayor que son las clases, una clase es, por así decirlo, la plantilla de un objeto, por ejemplo, se tiene la clase vehículo, un vehículo tiene diferentes atributos y métodos, estos atributos pueden ser la marca, el color, el modelo, etc. y los métodos son las acciones o funcionalidades que puede realizar este vehículo, como arrancar, frenar, acelerar, etc. Teniendo esta clase o plantilla, se pueden crear otros vehículos que heredarán estos atributos y métodos pero estos nuevos vehículos u objetos pueden modificar estos dependiendo de lo

 Aplicación del álgebra matricial para la solución de sistemas de ecuaciones lineales Matriz:  Es una disposición de valores numéricos y/o variables (representadas por letras), en columnas y filas, de forma rectangular. Una matriz es un arreglo bidimensional de números consistente en cantidades abstractas que pueden sumarse y multiplicarse entre sí. Una matriz es una tabla cuadrada o rectangular de datos (llamados elementos o entradas de la matriz) ordenados en filas y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales de la matriz. A una matriz con m filas y n columnas se le denomina matriz m x n; y a m y n se les denomina dimensiones de la matriz. Determinante de una matriz:   El determinante de una matriz de dimensión mxn es el resultado de restar la multiplicación de los elementos de la diagonal principal con la multiplicación de los elementos de la diagonal secundaria.  Método Gauss-Jordan:  Este método e

 Solución sistema ecuaciones método de Gauss-Jordan Documento del paso a paso:  https://drive.google.com/file/d/1au_GGixszdGyjVM45VPXYc5mrqHcR4bL/view?usp=sharing Diferencia entre el método Gauss y el Gauss-Jordan: Las diferencias entre ambos métodos es que el método Gauss se reduce la matriz de tal manera de que quede un sistema escalonado de filas y variables de las matrices, esto se logra reduciendo las posiciones de la triangular inferior a 0s, de esta manera en la fila 3 queda 1 variable con su coeficiente, en la fila 2 quedan 2 variables con sus coeficientes y en la fila 1 quedan 3 variables con sus coeficientes, al resolver el valor de la variable en la fila 3 se puede encontrar el valor de la variable de la fila 2 y con estás 2 se puede resolver la variable de la fila 1.  El método Gauss-Jordan es diferente y un poco más directo con su final pero al igual que el método Gauss se logra haciendo operaciones entre filas. En el método Gauss-Jordan se debe reducir la matriz hasta que

 Funciones Como persona y como profesional el conocimiento sobre funciones me permite solucionar problemas cotidianos de una manera más fácil y precisa, en el ámbito laboral este conocimiento me puede ayudar mucho para crear algoritmos que sean más eficientes y rápidos y así lograr mejores resultados dependiendo de lo que se este haciendo.